Desde que Alejandro Magno tomó la decisión fácil de deshacer el famoso nudo Gordiano cortándolo con un golpe de su espada en vez de tratar de desbaratarlo manualmente (lo cual muchos intentaron y fracasaron), los nudos han cautivado la atención de la humanidad, como lo muestra el siguiente mosaico en la villa de Piazza Armerina en Sicilia que data del Siglo IV:
Comenzaré esta charla señalando que hay muchas variedades de nudos. A continuación se tiene unos ejemplos de los nudos más sencillos que se conocen:
El primer hecho fundamental que podemos asentar es la existencia de lo que podríamos llamar nudos equivalentes. Dos nudos son equivalentes entre sí cuando, sin cortar la cuerda, podemos obtener un nudo del otro mediante simples operaciones manuales. Tomemos por ejemplo el siguiente nudo:
Invito a quienes estén leyendo este artículo a que se consigan un pedazo de cuerda y construyan el nudo anterior. Una vez que lo hayan hecho, los invito nuevamente a que, sin cortar la cuerda y utilizando operaciones manuales elementales, conviertan el nudo anterior en el siguiente "nudo", el nudo más sencillo y más elemental de todos los nudos, al cual podríamos llamar el "nudo trivial", el equivalente del número 1 de la aritmética que multiplicado por cualquier otro número nos dá el mismo número:
En virtud de que, sin necesidad de tener que cortar la cuerda, podemos obtener un nudo del otro, tenemos aquí un ejemplo claro de dos nudos equivalentes. Ambos son la misma cosa, aunque superficialmente no lo parezcan. Si estuvieramos hablando en términos de álgebra común y corriente para números, esto sería como escribir la expresión algebraica a=b. (En matemáticas, tenemos una palabra elegante para describir nudos que son equivalentes entre sí, nudos que pertenecen esencialmente a la misma clase. La palabra es isotopía, la cual se tomó prestada de los textos de química en los cuales se utiliza dicha palabra para referirse a las manifestaciones de lo que es básicamente un mismo elemento químico: los isótopos del elemento. Del mismo modo, cuando dos nudos son realmente el mismo nudo, decimos que son isótopos el uno del otro.) Puesto que tenemos ya la existencia del nudo más básico y elemental de todos, el "nudo trivial", como punto de partida, y tenemos el concepto de la equivalencia de nudos, aquí podemos tener ya un atisbo de que tal vez sea posible desarrollar una aritmética e inclusive un álgebra de nudos. A continuación tenemos otro ejemplo de cómo a partir del nudo conocido como "figura ocho" (por razones obvias) podemos obtener otros dos nudos que parecen ser diferentes y que sin embargo son lo mismo:
Para formalizar el concepto de la deformación de un nudo convirtiéndolo en una representación planar distinta del mismo, una de las primeras herramientas desarrolladas fueron las tres movidas Reidemeister, las cuales son operaciones fundamentales sobre un nudo llevadas a cabo sobre el mismo sin necesidad de tener que cortar la cuerda. Así tenemos la movida Reidemeister de Tipo I:
y la movida Reidemeister de Tipo II:
y la movida Reidemeister de Tipo III:
En 1928, el matemático Kurt Reidemeister, el autor del primer libro acerca de la teoría matemática de los nudos, Knottentheorie, demostró que dos diagramas planos de nudos aparentemente diferentes pero pertenecientes al mismo nudo siempre pueden ser relacionados entre sí mediante una secuencia de las movidas Reidemeister, lo cual intuitivamente resulta obvio si tenemos un pedazo de cuerda a la mano. Esto se conoce como el Teorema de Reidemeister, que afirma: "Sin podemos obtener un nudo del otro mediante la manipulación continua de un nudo en el espacio tridimensional, sin cortarlo, entonces podemos obtener el mismo resultado mediante una manipulación en la proyección sobre un plano del nudo que se lleve a cabo usando únicamente una de las tres movidas Reidemeister". A continuación tenemos una aplicación del teorema, en donde se puede ver cómo a través de una sucesión de movidas Reidemeister se reduce el nudo inicial al nudo trivial (he tomado algunas figuras del libro Knots del matemático ruso Alexei Sossinsky.):
Este teorema es importante porque reduce el problema de la definición y manipulación de un nudo de tres dimensiones a dos dimensiones. Las movidas Reidemeister vuelven a aparecer en la definición de las invariantes de nudos. Si podemos encontrar (y demostrar) una propiedad en un diagrama de nudo que no se altera cuando aplicamos un movimiento Reidemeister, podemos definir una invariante de nudo. Es así como se han definido variantes importantes, tales como el polinomio de Jones.
Puesto que hay muchos tipos de nudos que no son equivalentes, como los que vimos al principio, el primer paso lógico sería empezar con una clasificación rigurosa de los mismos. El nudo más sencillo de todos es indudablemente el "nudo de tres-hojas", del cual hay dos variantes: el de "mano izquierda" y el de "mano derecha":
Hay nudos que pueden ser omitidos de las tablas porque pueden construídos a partir de otros nudos más sencillos. Un ejemplo de ello es el nudo cuadrado:
A continuación tenemos una tabla que contiene clasificados nudos que definitivamente podemos considerar como "nudos primos":
Este tipo de representar diagramáticamente una clasificación de nudos no es la única manera posible. A continuación tenemos otra forma de hacerlo:
Las anteriores representaciones son representaciones "planas" de cada nudo en cuestión, son las imágenes (o mejor dicho, sombras) que proyectaría cada nudo tridimensional como los siguientes:
sobre una hoja de papel al iluminar cada uno de los nudos con una luz adecuada. El primer nudo de los que se muestran arriba, el cual está clasificado con un número principal de "4" y un número subscripto de "1", si lo examinamos detenidamente en su representación "plana", podemos ver que tiene cuatro "encuentros" o "cruces" en los cuales un segmento de la cuerda pasa ya sea por encima o por debajo de otro segmento de la cuerda. Este es el significado de ese número principal. Del mismo modo, el siguiente nudo, el segundo, tiene seis "cruces", por lo tanto su número principal es "6". Y el tercer nudo tiene ocho encuentros o "cruces", por lo tanto su número principal es "8". El lector puede comprobar por sí mismo la validez de los demás números principales ligados a cada nudo. Estos últimos nudos son unos nudos que llamamos "nudos anfiquirales", los cuales tienen la propiedad interesante de que, sin necesidad de tener que cortar el nudo, mediante operaciones elementales manuales es posible "convertir" cada uno de estos nudos en su imagen simétrica de "espejo", o sea el nudo que veríamos si pusieramos cada uno de estos nudos frente a un espejo. Invito a los lectores a que se consigan un pedazo de cuerda, uniéndolo para formar cada uno de los nudos arriba señalados, y jugar un poco para obtener su imagen "espejo", lo cual puede resultar entretenido (¿quién dijo que las matemáticas tenían que ser aburridas?)
Existe disponible en Internet el equivalente a un "atlas" que contiene la clasificación de nudos con hasta diez "cruces" (crossings): la Tabla de Nudos Rolfsen puesta en el siguiente enlace por el departamento de matemáticas de la Universidad de Toronto:
http://katlas.math.toronto.edu/wiki/The_Rolfsen_Knot_Table
La página principal de entrada a éste "atlas" es la siguiente:
http://katlas.math.toronto.edu/wiki/Main_Page
El interés científico en los nudos comenzó cuando el eminente físico-matemático irlandés William Thomson, mejor conocido como Lord Kelvin, propuso en 1860 una teoría interesante. Ya desde aquél entonces se sabía que la materia no era divisible hasta el infinito, se sabía que había un límite hasta el cual la materia podía ser dividida, ese límite era postulado como el átomo (del griego a="no" y tomos="división"). Esto es lo que conocemos como la teoría corpuscular de la materia, formada por esos pequeños corpúsculos llamados átomos. Pero también se sabía que la materia bajo ciertas condiciones exhibía un comportamiento que se manifestaba en vibraciones ondulatorias. Ambos conceptos serían unificados mucho tiempo después por lo que hoy se conoce como mecánica cuántica. Pero en aquél entonces, a Lord Kelvin se le ocurrió una posibilidad interesante. Propuso que, puesto que los átomos para cada elemento químico son diferentes de un elemento a otro, había la posibilidad de que cada átomo formase un "nudo" consigo mismo, el cual sería en efecto una cuerda vibrante. De este modo, cada elemento químico estaría representado por su propio nudo. Según Lord Kelvin, estos nudos elementales debían poder unirse entre sí traslapándose de alguna manera, formando nudos más complejos, o sea compuestos químicos como el agua y el dióxido de carbono. De acuerdo con la conjetura de Lord Kelvin, el átomo más elemental de todos, el átomo de hidrógeno, tal vez podría tener su equivalente en el "nudo trivial", mientras que los isótopos del hidrógeno (deuterio y tritio) podrían ser una variante del "nudo trivial". Siguiendo su conjetura, los siguientes "nudos atómicos":
podrían representar, respectivamente, una molécula formada por dos o tres elementos (tal vez , una molécula de agua, siendo el nudo central el átomo de oxígeno y los dos nudos laterales átomos de hidrógeno), un elemento más complejo que el átomo de hidrógeno elemental, y una molécula formada por dos elementos. Ciertamente, la idea de que un átomo se pueda eslabonar a otro átomo, encadenándose ambos entre sí como lo harían dos nudos entrelazados, explicaría la gran estabilidad de muchos compuestos químicos, sobre los cuales se requiere un estímulo energético intenso, ya sea calorífico o eléctrico, para romper el enlace y poder descomponer la molécula en sus elementos esenciales, o en este caso, en sus "nudos" fundamentales.
Alentado por la propuesta de Lord Kelvin, un físico-matemático escocés contemporáneo suyo, Peter Guthrie Tait (famoso por sus trabajos en el desarrollo de los cuaternios, lo cual condujo directamente al desarrollo del análisis vectorial tan importante para el desarrollo de la física-matemática moderna), llevó a cabo el primer paso fundamental para la construcción de una teoría de los elementos y compuestos químicos suponiendo la existencia de los mismos como nudos tridimensionales: la clasificación de los nudos. Tras llegar a la conclusión de que un nudo, definido como una curva cerrada (continua) en el espacio, puede ser representado como una curva en un plano proyectándolo perpendicularmente sobre un plano horizontal:
lo primero con lo que se topó fue que este tipo de representación (en un plano) adolece el defecto de que, suponiendo al nudo como una cuerda elástica, cada nudo puede tener varias representaciones con distintas cantidades de "cruces". A continuación tenemos dos representaciones planas, distintas, con distinto número de "cruces" (cuatro y trece cruces), del mismo nudo, deformado de la manera en que se muestra (sin cortar la cuerda):
Es por esto que, al clasificar un nudo, se busca la proyección del mismo en un plano que tenga la menor cantidad posible de "cruces". Aunque el crédito por la elaboración de la primera clasificación de nudos con hasta diez cruces se le dá a Tait (lo cual le consumió el resto de su vida), pudo empezar a partir de una clasificación preliminar que ya había sido hecha por un matemático amateur, el Reverendo Thomas Kirkman, el cual ya había hecho una clasificación de curvas con la menor cantidad posible de "cruces". El problema se reducía a eliminar las repeticiones en el plano de un mismo nudo, para no repetirlo dentro de la tabla. Para simplificar su labor, Tait decidió enlistar únicamente los nudos alternantes, aquellos en los cuales la hebra del nudo va pasando, en forma alternada, por encima y por debajo de los otros segmentos del nudo con los que se va encontrando. A continuación tenemos un ejemplo de un nudo no-alternante, lo cual es más que obvio al ver la parte inferior:
La clasificación de los nudos no-alternantes quedaría a cargo de C. N. Little, quien lo logró en 1899 tras seis años de esfuerzos.
Sin embargo, la teoría de representar a los átomos y las moléculas como nudos básicos uniéndose entre sí para formar nudos más complicados se estancó en definitiva cuando el ruso Dimitri Mendeleiev concibió la tabla periódica de los elementos, la cual demostró una utilidad mucho mayor para clasificar las propiedades químicas y eléctricas de los elementos así como la capacidad para poder formar moléculas entre sí de acuerdo con su posición en la tabla periódica. Y mucho tiempo después el advenimiento de la mecánica cuántica explicaría las razones de los agrupamientos de los elementos observados en la tabla periódica. De aquí en adelante, el interés por la teoría de nudos quedaría exclusivamente en manos de los matemáticos, y no sería sino hasta mediados del Siglo XX cuando los nudos volverían a encontrar aplicaciones en el campo de la física, como la teoría topológica de los campos cuánticos (TQFT, la abreviatura en inglés de la frase "Topological Quantum Field Theory").
Una vez que tenemos una "tabla" de nudos elementales, podemos llevar a cabo lo que vendría siendo una aritmética de nudos. Del mismo modo en que un número que no sea un número primo (como 5, 7, y 13) se puede descomponer en el producto de dos números (por ejemplo, 15 que se puede descomponer como el producto de 3 y 5), un nudo aparentemente complejo tal vez pueda ser descompuesto, sin cortar la cuerda, en sus "factores primos" de la forma en la que se muestra a continuación:
El proceso inverso no representa dificultad alguna. Tomando dos nudos cualesquiera de una tabla de nudos, podemos formar un nudo compuesto en la forma que se muestra a continuación:
Uno de los avances importantes en la teoría matemática de los nudos que demuestra cierta similitud con descubrimientos hechos en otras ramas de las matemáticas es el que fue hecho en 1949 por el matemático Horst Schubert, quien demostró que, así como en la teoría de los números cualquier número siempre se puede factorizar de una sola manera como un producto de números primos (lo cual en muchos textos se conoce como el Teorema Fundamental de la Aritmética, teorema del que podemos encontrar dos demostraciones básicas en el libro What is Mathematics? de Courant y Robbins), por ejemplo:
121501138 = 2*3*7*7*11*13*17*17
también un nudo compuesto siempre se puede descomponer en una composición única de "nudos primos".
Antes de continuar, veamos una rama de las matemáticas que está estrechamente ligada a la teoría matemática de los nudos: la teoría de las trenzas, en donde al hablar de trenzas estamos hablando de algo literalmente similar a las trenzas de las niñas de secundaria o la trenza con la que está hecha un látigo o la reata de un vaquero. A continuación tenemos tres ejemplos de trenzas, dos trenzas de tres hilos y una trenza de cinco hilos:
También como en el caso de las cuerdas, podemos construír "tablas" para la clasificación de las trenzas. A continuación tenemos una clasificación de los varios tipos de trenzas de cuatro hilos, siendo la trenza más elemental, la "trenza trivial" por así decirlo, la que aparece en el extremo inferior izquierdo:
La diferencia fundamental entre un nudo y una trenza es que a un nudo lo podemos considerar como una cuerda continua sobre la cual si una pulga empieza a caminar en una sola dirección eventualmente volverá a su punto de partida, mientras que una trenza no forma un camino cerrado, cada hilo de la trenza tiene un principio y un final.
Al construír una tabla de trenzas "fundamentales", hay que tener cuidado de no incluír dos trenzas que, en apariencia distintas, con una manipulación de las cuardas sin mover en lo absoluto los puntos extremos de sus posiciones originales se puedan obtener la una de la otra. Porque es el caso que, al igual que como sucedió con los nudos, también tenemos lo que podemos llamar los isótopos de una trenza. En los siguientes dibujos tenemos el ejemplo de cómo la trenza del extremo izquierda se puede transformar en la trenza del extremo derecho (o viceversa) efectuando los movimientos que se muestran en el dibujo intermedio:
Como en el caso de los nudos, frecuentemente estamos interesados en simplificar una trenza hasta su expresión mínima, lo cual significa que sin cortar con tijeras ninguno de los hilos de la trenza y efectuando algo similar a los movimientos Reidemeister que llevamos a cabo sobre las proyecciones planares de los nudos, obtenemos una trenza isotópica con la menor cantidad posible de "cruces". A continuación tenemos dos ejemplos de trenzas simplificadas hasta su mínima expresión:
En este ejemplo, tomamos la trenza del extremo izquierdo y la pusimos sobre la trenza del centro, formando la trenza compuesta que aparece en el extremo derecho. Obsérvese que si hubiéramos tomado la trenza del centro poniéndola sobre la trenza del extremo izquierdo, habríamos obtenido una trenza compuesta diferente a la que obtuvimos arriba. Esto demuestra un hecho importante: a diferencia de la aritmética de los números en donde el orden de los factores no altera el producto, en la aritmética de las trenzas el orden de los factores sí altera el producto.
Como ya se mencionó, al igual que en la aritmética básica en donde tenemos el número uno, tenemos también la trenza unitaria, o sea la trenza trivial, cuyos hilos cuelgan todos ellos verticalmente sin cruzarse. Esta es la trenza cuyo "producto" con otra trenza nos produce la misma trenza. Más interesante aún es el hecho de que, para cada trenza, existe una trenza inversa, cuyo "producto" con dicha trenza nos dá la "trenza unitaria". Es muy fácil obtener la trenza inversa de cualquier otra trenza, puesto que la trenza inversa no es más que el reflejo en un espejo de la trenza original. A continuación tenemos un ejemplo de cómo una trenza "multiplicada" por su trenza inversa nos produce la trenza unitaria:
No es difícil ver que, dadas tres trenzas, a, b y c, con la misma cantidad de hilos, podemos "multiplicar" las tres trenzas siguiendo dos secuencias diferentes. De la primer forma, conectamos primero la trenza a con la trenza b y tras esto conectando la trenza así obtenida con la trenza c, lo cual podemos simbolizar como (a•b)•c. Siguiendo una secuencia diferente, podemos conectar la trenza b con la trenza c primero y tras esto unir dicho "producto" a la trenza a, simbolizado como a•(b•c). El resultado final en ambos casos será el mismo. Esto es lo que llamamos la asociatividad del producto de las trenzas, simbolizado para tres trenzas como:
(a•b)•c = a•(b•c) Propiedad asociativa del producto de las trenzas
Puesto que, en la aritmética de las trenzas, tenemos la existencia de una trenza unitaria, así como la existencia de una trenza inversa, así como el cumplimiento de la propiedad asociativa al tomar el producto de varias trenzas, se cumplen todas las condiciones para lo que en matemáticas se define como un grupo, al cual le podemos aplicar todos los teoremas que se conocen en la teoría de grupos, la cual es extensa. Es importante observar a estas alturas que el producto de dos trenzas no es conmutativo, o sea que no se cumple la condición de que el producto a•b nos produzca el mismo resultado que el producto b•a, ya que una de las trenzas la podemos unir a la otra colocándola por encima de ella o bien por debajo de ella, y en ambos casos el resultado serán dos trenzas compuestas distintas. Pone la trenza a sobre la trenza b no nos produce la misma trenza que si ponemos la trenza b sobre la trenza a. Con esto, acabamos de demostrar que las trenzas con la misma cantidad de hilos forman un grupo no-conmutativo.
Volvamos ahora a la aritmética de las nudos. Una pregunta que podemos responder de inmediato es acerca de la propiedad asociativa de la composición de dos o más nudos. ¿Tienen los nudos esta propiedad? ¡Claro que sí! Si representamos la operación de composición de dos nudos con el símbolo #, entonces la propiedad asociativa para una composición de tres nudos sería:
(a#b)#c = a#(b#c) Propiedad asociativa de la composición de los nudos
Esto todo lo que nos dice es que, si a lo largo de un hilo, formamos dos nudos a y b, y tras esto agregamos un tercer nudo c, siguiendo el mismo orden para irlos agregando, entonces obtendríamos lo mismo si primero formamos un nudo compuesto con los nudos b y c, y tras esto lo agregamos (manteniendo el mismo orden) al nudo c.
Ya mencionamos la existencia del "nudo trivial" o nudo unitario, el nudo más básico de todos, el cual equivale al número 1 en la aritmética, cuya composición con cualquier otro nudo dejará al otro nudo inalterado. Puesto que existe el nudo unitario, y se cumple la propiedad asociativa para la composición de los nudos, esto nos lleva a sospechar en la posibilidad de que también pueda haber un nudo inverso, un nudo cuya inclusión tendría una propiedad extraordinaria: al meter en una pedazo de cuerda un nudo y su inverso, el nudo inverso cancelaría al nudo original produciendo el nudo unitario, o sea que al jalar los extremos de la cuerda ambos nudos desaparecerían. Esto nos permitiría clasificar a los nudos como un grupo. Sin embargo, esto no es posible, porque los nudos inversos no existen, al igual que en la aritmética de los números naturales mayores que uno (2,3,4,5,6,7,8, etc.) en donde no existe un número n que multiplicado por un número m nos dé como resultado el número 1. Podemos dar una demostración sencilla de esto por contradicción, suponiendo que los nudos inversos sí existen. En tal caso, supóngase que un nudo a es el inverso de un nudo b. Si es así, entonces la composición de ambos nudos nos debe producir el nudo unitario, o sea:
a#b = 1
Imaginemos ahora que tenemos una cuerda infinitamente larga y que dentro de ella tenemos, uno tras otro, un nudo a seguido de un nudo b, formando un nudo compuesto C:
C = a#b#a#b#a#b#...
Por la propiedad asociativa, la cual ya vimos que se cumple en la aritmética de los nudos, podemos agrupar este "producto" de nudos en "subp-productos" de la siguiente manera:
C = (a#b)#(a#b)#(a#b)#...
C = 1#1#1#...
C = 1
C = 1#1#1#...
C = 1
De este modo, esta composición infinita de nudos se simplifica al nudo unitario. Pero la misma propiedad asociativa nos permite agrupar los "nudos primos" de la siguiente manera:
C = a#(b#(a)#(b#a)#...
C = a#1#1#1...
C = a
C = a#1#1#1...
C = a
Los dos resultados nos llevan a la conclusión de que a = 1, lo cual contradice la suposición de que a era un nudo no-trivial. En otras palabras, el único nudo inverso posible es el nudo unitario. Esta falta de la existencia de un nudo "inverso" es lo que nos impide clasificar a los nudos como un grupo matemático.
El argumento dado aquí no es un argumento estrictamente formal por el hecho de que estamos haciendo uso de una secuencia infinita de nudos elementales. Sin embargo, el argumento se puede formalizar de modo riguroso haciendo cada nudo a lo largo de la cuerda más y más pequeño que el nudo anterior, haciendo que la composición no se extienda hacia el infinito sino que converja hacia un nudo límite. De este modo, recurriendo a la definición de límite, el argumento se hace formal. Esto es precisamente lo que se hace en la topología. Es esta la razón por la cual se usa tanto el concepto de límite en esa rama de las matemáticas.
Además de que una aritmética de nudos posee la propiedad asociativa, en la composición de dos nudos también se cumple la propiedad conmutativa. En la siguiente figura podemos ver cómo la operación de composición no depende del orden en el cual están puestos los nudos "primos", ya que sin necesidad de tener que cortar la cuerda con unas tijeras, deslizando el nudo situado en el extremo izquierdo en la forma amañada como se muestra (haciéndolo chiquito primero, lo cual no altera la naturaleza de dicho nudo ya que sigue siendo el mismo) a lo largo del nudo que le sigue, seguimos teniendo el mismo nudo compuesto.
Un teorema importante nos dice que siempre es posible convertir una trenza en un nudo. Intuitivamente esto no presenta dificultad alguna, todo lo que tenemos que hacer es "conectar" los extremos opuestos de una trenza de alguna manera para obtener de inmediato un nudo. En las figuras que se muestran a continuación, tenemos a la izquierda una "trenza", y a la derecha un nudo obtenido a partir de dicha trenza:
Al hacer esta operación de obtener un nudo a partir de una trenza, hay fijarse muy bien en lo que se está obteniendo. A continuación se muestran dos trenzas (a) y (b) en el proceso de ser convertidas en nudos:
Obsérvese bien que en el caso de la trenza (a) obtenemos un nudo que, si el lector pone atención, comprobará que se trata del "nudo de tres-hojas" que ya vimos con anterioridad. En cambio, en el caso de la trenza (b), en lugar de obtener un nudo (el cual por definición está formado por una sola cuerda) obtenemos un eslabón de dos componentes.
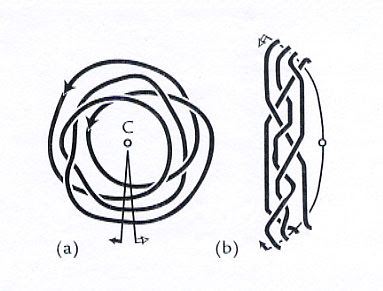
Puesto que un trenza puede ser transformada en un nudo, esto nos plantea una pregunta interesante: ¿Cuáles nudos podemos obtener a partir de las trenzas ya conocidas? Esta pregunta fue respondida por en 1923 por el matemático norteamericano J. W. H. Alexander, quien demostró algo mucho más general: Todos los nudos conocidos, habidos y por haber, incluyendo los que muchos faltan por descubrir, se pueden representar como trenzas "cerradas" (convertidas en nudos). Este teorema parte de otro hecho que también requiere una demostración rigurosa: cualquier tipo de nudo, el que sea, puede ser convertido en una trenza circular cerrada, como nos lo dice el siguiente poster:
Un visualización elemental de este hecho la tenemos en el siguiente diagrama:
Y de hecho, la parte "difícil" de una demostración del teorema de Alexander de que siempre se puede obtener un nudo a partir de una trenza se centra en el hecho de que, como nos lo indica el poster arriba citado, siempre se pueda convertir un nudo cualquiera en un "rollo" circular, porque si esto es posible, entonces basta con "cortar" el rollo transversalmente como se muestra a continuación para obtener la trenza capaz de producir dicho nudo siguiendo una secuencia inversa en las operaciones:
Desafortunadamente, la demostración rigurosa, formal, de que siempre es posible obtener un nudo a partir de una trenza, es algo que requiere de argumentos matemáticos sumamente sofisticados que nos llevan directamente al campo de la topología, otra área avanzada de estudio de las matemáticas. Pero aquí le hemos dado una idea al lector de cómo se puede llevar a cabo la demostración; todo lo demás son "detallitos".
Al estar trabajando con nudos, podemos definir el "interior" de un nudo (¡mucho cuidado con lo que queremos decir por el "interior" de un nudo!) en una forma similar a como definiríamos el interior de una circunferencia. El interior de una circunferencia es, desde luego, un círculo. Puesto que el nudo unitario (o nudo trivial) puede ser deformado fácilmente para tomar la forma de una circunferencia al ser proyectado sobre un plano, debe resultar obvio que dentro del nudo unitario debe ser posible montar una membrana elástica que podríamos definir como la "superficie" interna a dicho nudo. Pero no sólo podemos montar una membrana elástica al interior de un nudo unitario. También podemos hacerlo con otros nudos. Por ejemplo, al hacerlo con el "nudo de tres-hojas" como el que se muestra a continuación:
obtenemos algo como lo siguiente:
Esta no es la única "superficie" que podemos obtener de dicho nudo. Hay otra superficie obtenible del mismo nudo. Es la siguiente:
A continuación tenemos otra vista de esta ultima superficie:
Ahora construiremos una superficie para el "nudo figura ocho":
Es la siguiente:
Todas estas superficies o "membranas" tienen un nombre. Se llaman superficies de Seyfert. Los ejemplos que hemos visto deben ser suficientes para comprender la definición formal de una superficie Seyfert: Una superficie Seyfert es una superficie orientada, acotada por un nudo o un eslabón. Las superficies Seyfert mostradas se pueden obtener con una herramienta desarrollada por la universidad holandesa Technische Univeriteit Eindhoven denominada SeifertView, la cual se puede descargar gratuitamente del siguiente enlace:
http://www.win.tue.nl/~vanwijk/seifertview/
Como vimos en el caso de la superficie Seyfert para el "nudo de tres-hojas", un mismo nudo (o eslabón) puede tener más de una superficie Seyfert, las cuales no son equivalentes entre sí.
Existe un teorema que nos dice que, para cualquier tipo de nudo, siempre existirá por lo menos una superficie Seyfert que se pueda montar sobre dicho nudo. Aunque el teorema fue demostrado por vez primera por el matemático ruso Lev Pontryagin (el mismo que dejó un famoso teorema de maximización que es hoy fundamental en el estudio de la Teoría Moderna de Control, y el cual logró todas sus espectaculares contribuciones pese a que quedó ciego a los 14 años de edad), el crédito se le concede a Herbert Seifert porque además de publicar en 1934 otra demostración del teorema inventó también un procedimiento para generar dichar superficies.
Una ayuda importante para el estudio de los nudos lo proporcionan las computadoras que tengan instalado un programa como Mathematica, con el cual se pueden generar diagramas tridimensionales de nudos como los siguiente correspondiente al nudo "figura ocho":
El programa Mathematica no sólo puede generar diagramas tridimensionales de nudos. También puede responder a preguntas específicas. Por ejemplo, entre la lista de comandos disponibles dentro de Mathematica, existe el comando KnotData, el cual puede recibir uno o dos argumentos. Si proporcionamos en la línea de entrada la siguiente instrucción:
In[1]:=KnotData["Threefoil"]
entonces al usar la instrucción Out[1] para obtener una respuesta, Mathematica dibujará el siguiente diagrama tridimensional del "nudo de tres-hojas":
Al igual que ciertas figuras geométricas o ciertos cristales sólidos que poseen alguna propiedad distintiva que no poseen los demás miembros de sus familias, también algunos nudos poseen ciertas características interesantes que los hacen diferentes de los demás. Ya vimos que una de ellas es la propiedad de ser nudos primos, no pueden ser obtenidos a partir de nudos más elementales que ellos. Otra de tales características es la que conocemos como la anfiquiralidad, la propiedad de que, sin cortar el nudo para nada, manipulándolo mediante operaciones manuales elementales, podemos obtener la imagen simétrica de "espejo" que corresponde al nudo original, o sea el nudo que veríamos al poner el nudo original reflejado frente a un espejo. Usando el programa Mathematica, podemos obtener información sobre si cierto nudo del cual tenemos su nombre en la base de datos de Mathematica es o no es anfiquiral, con una instrucción como la siguiente:
KnotData["Threefoil", "Amphichiral"]
Una herramienta importante para la clasificación de los nudos son los llamados "polinomios" usados para representar nudos, de los cuales existen varios. A continuación, para el nudo "figura ocho" que acabamos de ver, tenemos de arriba a abajo, el polinomio Alexander (el primero en ser descubierto, en 1928), el polinomio BM/Ho, el polinomio Conway (el cual por ser una versión modificada del polinomio Alexander a veces es designado como el polinomio Conway-Alexander), el polinomio HOMFLY (Hoste Ocneanu Millett Freyd Lickorish Yetter, los descubridores simultáneos del polinomio), el polinomio Jones (el segundo polinomio en ser descubierto, en 1984) y el polinomio Kauffman:
Cada uno de estos polinomios tiene sus ventajas y sus desventajas. De nueva cuenta, usando el programa Mathematica, podemos generar este tipo de polinomios para cada nudo en particular. Por ejemplo, si queremos generar el polinomio Alexander para el "nudo de tres-hojas", lo podemos hacer usando la siguiente instrucción en Mathematica:
In[1]:=KnotData["Threefoil", "AlexanderPolynomial"][x]
Como vimos en uno de los dibujos anteriores, hay de hecho dos nudos "de tres-hojas", uno de "mano izquierda" y uno de "mano derecha". Pero la representación en ambos casos utilizando el polinomio Alexander (así llamado en honor a su descubridor, el matemático norteamericano J. W. Alexander) hay uno solo polinomio para las dos variantes del "nudo de tres-hojas", como nos lo comprueba el programa Mathematica. Esto quiere decir que el polinomio Alexander es incapaz de distinguir entre un "nudo de tres-hojas" de "mano izquierda" y un "nudo de tres-hojas" de "mano derecha". Esta deficiencia al nivel más básico permite suponer que el polinomio Alexander tampoco será capaz de distinguir entre otros pares de nudos más complejos a los que, pese a ser diferentes, les asignará el mismo polinomio. Esta desventaja es lo que dió origen a la búsqueda de nuevos polinomios, cada uno de los cuales trae consigo nuevas ventajas así como nuevas deficiencias. Estos "polinomios" no son polinomios en el sentido tradicional del álgebra que se enseña en las escuelas secundarias en donde uno puede substituír valores numéricos para una incógnita "x". Son polinomios simbólicos usados para representar nudos con otro concepto fundamental de uso detrás de todos ellos: si dos nudos tienen la misma "fórmula", el mismo polinomio, usado bajo cierto esquema (Alexander, HOMFLY, etc.), entonces ambos nudos son equivalentes entre sí, son la misma cosa. Aunque las figuras tridimensionales generadas por computadora son excelentes para visualizar nudos, son de muy poca utilidad para saber, a primera vista, o inclusive bajo inspección cuidadosa, si dos nudos que parecen diferentes son esencialmente lo mismo, aún teniendo una cuerda a la mano para poder jugar con dicha cuerda formando uno de los nudos y tras esto tratar de obtener el otro nudo. Para ello, necesitamos una representación simbólica de cada nudo, algo que podamos escribir en el papel, capaz de representar de manera única al nudo en la forma más general y más concisa posible, una representación abstracta (generalizada) de los nudos. En pocas palabras, una representación matemática. Es aquí en donde entran los polinomios simbólicos de los nudos, para esto fueron creados (o mejor dicho, descubiertos).
Antes de continuar, tenemos que mencionar aquí una convención que se utiliza frecuentemente en el estudio de los nudos al ser proyectados horizontalmente sobre un plano. Es la convención del signo de un cruce, la cual nos dice que en un nudo a lo largo de cuya cuerda hemos fijado una dirección de recorrido (moviéndonos siempre en la misma dirección hasta volver al punto de partida, simbolizado por una flecha o flechas apuntando a lo largo de la cuerda) el cruce positivo (+1) es aquél para el cual una pulga que está caminando a lo largo de la parte superior de un segmento que se encuentra que se encuentra con otro ve a la flecha del segmento inferior apuntando hacia la izquierda, mientras que el cruce negativo (-1) es aquél para el cual una pulga que está caminando a lo largo de la parte superior de un segmento que se encuentra con otro ve la flecha del segmento inferior apuntando hacia la derecha, tal y como se muestra en el siguiente diagrama:
Para aclarar aunque sea un poco el asunto de los polinomios de nudos, se darán a continuación algunos detalles sobre el polinomio de Conway, llamado así en honor al prolífico matemático inglés John Horton Conway (creador, entre otras cosas, del famoso "Juego de la Vida" o Game of Life que tanto furor causó en los años noventa cuando las computadoras fueron usadas para crear sobre una cuadrícula rectangular unos primitivos "seres" artificiales que, obedeciendo ciertas reglas dependientes de su propio valor y/o el de sus células vecinas, podían crecer y transformarse de forma casi inesperada, algo a lo cual se le conoce académicamente como autómatas celulares). Para construír su polinomio, Conway utilizó dos operaciones "quirúrgicas" que en un momento dado requieren cortar el nudo con tijeras para poder relocalizar los segmentos cortados, uniéndolos después con goma de pegar o Kola Loka. Estas operaciones están resumidas a continuación:
Obsérvese que en los "cruces" utilizamos la convención que habíamos definido anteriormente en relación a los signos de dichos encuentros. Una operación es la de "volteo" (flip), con la cual podemos "bajar" o "subir" uno de los hilos con respecto al otro, convertiendo el "cruce" de los segmentos de positivo (+) a negativo (-) o viceversa. La otra operación es de "suavización" (smoothing) con la cual podemos deshacer cualquiera de los cruces mostrados arriba en las figuras del extremo izquierdo y el extremo derecho reduciendo el cruce a lo que se muestra en la figura central, en donde ya no hay "encuentro" alguno, y en donde apropiadamente no hay signo asignado usándose para ello el número cero (0).
Una vez que se han definido estas operaciones básicas, el siguiente paso es asentar una fórmula que defina de alguna manera al polinomio Conway. Esta es la relación de "madeja" (skein) que se muestra a continuación (por cierto, el símbolo triangular usado aquí para denotar al polinomio es conocido comunmente como nabla, aunque aquí le pediré a mis lectores que cuando vean este símbolo simplemente lo relacionen con la palabra "polinomio", tal y como se acostumbra en los textos de la teoría de los nudos):
Por definición, el polinomio Conway de un nudo unitario (simbolizado a continuación como una curva circular cerrada) es la unidad:
Una vez definidas las operaciones básicas que podemos llevar a cabo sobre los "cruces" de un nudo, y definido el valor del polinomio para el nudo unitario, podemos asentar el propósito fundamental del polinomio, que es:
Estas tres relaciones de Conway son relaciones recursivas que se tienen que estar aplicando no una sino varias veces a un nudo complejo para irlo simplificando obteniendo nudos más "elementales" a partir del mismo, y al hacer esto el polinomio de Conway para el nudo complejo se va definiendo de manera casi automática. En realidad, es más fácil determinar primero los polinomios de Conway para los nudos más elementales, y usando dichos polinomios ir progresando hasta obtener el polinomio del nudo más complejo, en lo que viene siendo una mezcla de operaciones geométricas y algebraicas. A continuación llevaremos a cabo la obtención de algunos polinomios de Conway, progresivamente complejos, para darle a mis lectores una idea de cómo se obtienen dichos polinomios, y hacerles ver cómo una filosofía "constructiva" (yendo de lo más fácil hacia lo más difícil) puede ser una buena alternativa a una filosofía "reduccionista" (simplificando algo complejo hasta llegar a sus partes elementales). El primer polinomio que obtendremos será el polinomio para un nudo con un "cruce" sencillo, el cual se obtiene como se muestra a continuación:
Ahora llevaremos a cabo el cálculo del polinomio para dos nudos unitarios no-eslabonados (independientes). En este caso, sí usaremos la relación de madeja. La obtención del polinomio, paso por paso se da a continuación:
A continuación, llevaremos a cabo el cálculo del polinomio de Conway para el eslabón más sencillo que se conoce, formado por dos nudos unitarios eslabonados, lo cual se conoce como el eslabón Hopf, llamado así en referencia al matemático Heinz Hopf quien estudió sus propiedades. Mencionaremos de paso otro eslabón más interesante, el eslabón Borromeo, llamado así en referencia a la familia Borromeo que lo utilizó en Italia desde el siglo XII como su escudo de armas, formado por tres nudos unitarios entrelazados:
el cual tiene la propiedad de que si removemos cualquiera de los aros, los otros dos aros quedarán libres de inmediato.
La obtención del polinomio de Conway para el eslabón Hopf es la siguiente:
Estamos listos ya para la obtención del polinomio de Conway de un nudo un poco más elaborado, el "nudo de tres-hojas". Los pasos efectuados para ello son los siguientes:
Tal vez el lector quiera probar su suerte obteniendo el polinomio Conway para un nudo un poco más elaborado, como el polinomio del nudo "quinti-hojuela":
En los cursos universitarios de teoría de nudos, en las exposiciones en el pizarrón o al intercambiar notas, al llevar a cabo operaciones a veces se omite el triángulo invertido con el que representamos la palabra "polinomio" por ser obvia la alusión al mismo, como lo muestra la siguiente página de notas publicada en Internet sobre el polinomio Alexander en el cual en vez de usar la variable x usamos la variable z:
Es muy posible que todavía haya otros polinomios esperando a ser descubiertos. Ciertamente, la teoría matemática de los nudos todavía tiene un largo trecho por recorrer. Por lo pronto, hasa ahora, cada uno de los polinomios conocidos tiene su propio talón de Aquiles, para todos ellos hay algún nudo sencillo o complejo que erróneamente resulta ser equivalente (isotópico) a otro nudo diferente al tener ambos el mismo polinomio. En la búsqueda de algún otro tipo de invariante que nos permita clasificar de manera única todos los nudos que sean diferentes, uno de los avances recientes más importantes son las invariantes de orden finito, concebidas en 1990 por Victor Vassiliev, un matemático experto en la teoría de las singularidades, mejor conocida como la teoría de catástrofe.
Antes de continuar, trataré de dar una idea de dónde viene el concepto de "catástrofe", en su sentido matemático. Físicamente hablando, un punto carece de dimensiones en un espacio tridimensional, ya que define una posición exacta en el espacio. De no ser así, entonces sería algo como una esfera en lugar de un punto, y tendría un volumen definido. Por otro lado, una predicción de la Teoría General de la Relatividad son los hoyos negros, según la cual cuando hay una cantidad suficiente de masa junta, las fuerzas gravitacionales son de tal magnitud que todos los átomos empiezan a fusionarse entre sí hasta el infinito a grado tal que toda esa masa "desaparece" al ser comprimida hasta un punto matemático sin dimensiones. La masa, que puede ser de varios miles de millones de toneladas, sigue ahí, lo que pasa es que toda esa masa ha sido comprimida hasta un punto matemático ideal. Esto es lo que llamamos una singularidad física, un concepto que desafía nuestra intuición. Del mismo modo, en expresiones matemáticas, cuando hay algo que nos lleva a una división entre cero (por ejemplo, en la expresión de álgebra 1/(x-4) un valor de x igual a 4 nos produce una división entre cero), también tenemos una singularidad, en este caso una singularidad matemática.
Como lo define Vassiliev, en los nudos se produce una "catástrofe" o singularidad cuando una parte de un nudo en vez de pasar por encima o por debajo de otra, se cruza con ella, atravesándose ambos mutuamente por un instante, ocurriendo la catástrofe en el punto del encuentro. A continuación tenemos un ejemplo de una "catástrofe" como la define Vassiliev:
El cálculo de una invariante de Vassiliev, basado en la aplicación de la matemática combinatórica (tal y como lo pide la teoría de la catástrofe en la que Vassiliev es experto) hace uso de unos diagramas conocidos como diagramas de Gauss o diagramas de cuerdas, y su resultado final es, a fin de cuentas, algo que debe poder permitir distinguir a cualquier nudo de otro sin necesidad de andar haciendo dibujos (los cuales, aunque ilustrativos, no sirven de mucho para nudos muy complejos con muchos "cruces").
Cada invariante de Vassiliev le asigna tanto a los nudos ordinarios como a los nudos singulares (aquellos que tienen un punto doble) no un polinomio, sino un valor numérico que puede ser un entero positivo, negativo, o cero. Otra diferencia de las invariantes de Vassiliev con respecto a los polinomios es que un mismo nudo puede tener no una sino varias invariantes de Vassiliev dependiendo de la secuencia de operaciones que se lleven a cabo para obtener la invariante. La metodología para obtener una invariante de Vassiliev procede en forma similar a la que ya vimos para la obtención de los polinomios de nudos. Empezamos con un nudo como el "nudo de tres-hojas", seleccionamos un "cruce" (ya sea positivo o negativo), producimos una catástrofe (punto doble) tras lo cual queda invertido el cruce convirtiendo al nudo en otro que puede ser el nudo unitario. Existe una conjetura que hasta la fecha (2007) no ha podido ser demostrada ni refutada: Las invariantes de orden finito pueden ser utilizadas para clasificar todos los nudos posibles. De ser cierto, esto las haría superior a cualquiera de los polinomios usados para clasificar nudos, que han resultado incompletos.
La Tabla de Nudos Rolfsen puesta en Internet por el departamento de matemáticas de la Universidad de Toronto, cuyo enlace ya se proporcionó con anterioridad, contiene mucho más que las figuras correspondientes a cada uno de los nudos fundamentales que se conocen con hasta diez "cruces" en sus proyecciones sobre un plano. Pulsando sobre cada uno de los nudos, somos enviados a una página muchísimo más extensa en donde podemos ver listados los distintos tipos de polinomios para cada nudo sobre el cual deseamos obtener mayor información.
Una clase de nudos con propiedades interesantes es la que conocemos como los nudos toroidales, los cuales no son más que nudos que se pueden enrollar alrededor de una "dona" (en matemáticas preferimos utilizar la expresión toroide en lugar de la palabra vulgar "dona"), de los cuales tenemos el siguiente ejemplo (con un poco de imaginación es posible ver cómo este nudo se puede enrollar a lo largo de un toroide):
No entraré en detalles sobre el por qué puede ser ventajoso recurrir a una aparente complejidad, el enrollar un nudo alrededor de un toroide, para continuar con nuestro estudio de la matemática de los nudos. Me tendrán que creer cuando les digo que, pese a todo, hacer esta operación tiene enormes ventajas para llevar a cabo ciertas demostraciones de varios teoremas importantes.
Otra cosa que es importante agregar es el hecho de que, aunque en las matemáticas se pueden definir espacios multidimensionales que van más allá del espacio de las tres dimensiones que conocemos de largo, ancho y altura (Einstein usó un espacio de cuatro dimensiones para la construcción de la Teoría de la Relatividad), el matemático célebre matemático Klein demostró que los nudos no pueden existir en un espacio con una dimensión par, y desde entonces se ha demostrado también que ningún nudo puede existir en cualquier dimensión igual o mayor que cuatro. Lo cual, sin embargo, no ha sido impedimento alguno para que los conceptos de la teoría de los nudos estén encontrando aplicaciones importantes en el campo de la física teórica avanzada. La matemática de los nudos es en estos momentos objeto de estudio e investigación intensos, sobre todo ahora que varios avances permiten relacionar esta rama nuevamente con el campo de la física teórica, el lugar en donde comenzó originalmente con la propuesta de Lord Kelvin de que todos los átomos y las moléculas son esencialmente nudos de diversa índole. Una de dichas áreas es la de los "Grupos Cuánticos" (Quantum Groups). Los grupos cuánticos no son "grupos" en el sentido matemático de la palabra (un conjunto de elementos como el grupo de las trenzas, en donde para cada elemento del grupo hay un elemento inverso, y en donde se cumple la propiedad asociativa). Son en realidad álgebras de un tipo muy especial conocido como biálgebras. En una biálgebra definimos no una sino dos operaciones: la multiplicación y la comultiplicación. Para tener una idea generalizada de lo que es esto, recordemos la tabla de multiplicar de los números enteros. Esencialmente, lo que hace dicha tabla es asociar dos números a y b a otro número c. Por ejemplo, si nos mencionan los números 3 y 7, de inmediato los asociamos con el número 21. En la comultiplicación hay algo que funciona de modo inverso, ya que en tal caso si nos dan algo como el número 15, a partir de dicho número obtenemos dos números, los números 3 y 5. Las operaciones de multiplicación (en la cual dos cantidades se "funden" para producir una sola) y de comultiplicación (en la cual una sola cantidad se "descompone" para producir dos cantidades) corresponden precisamente a los procesos físicos de fusión y fisión atómica, esenciales para la construcción de reactores nucleares. Relacionado con todo esto, las matemáticas de las trenzas que vimos arriba tienen un impacto directo en una ecuación importante para la física moderna, la ecuación Yang-Baxter. Para académicos y universitarios: la relación existente entre la teoría de las trenzas y la física cuántica moderna se puede apreciar mejor en varias exposiciones que han sido colocadas por el profesor John C. Baez de la Universidad de California de Riverside en el siguiente enlace:
http://math.ucr.edu/home/baez/braids/
Otro campo activo de investigación en la teoría matemática de los nudos aplicada a la física es la Teoría Topológica de los Campos Cuánticos (TQFT, de sus siglas en inglés "Topological Quantum Field Theory"), de la cual de hecho hay varias y no una sola. La idea de una TQFT es estudiar, desde el punto de vista de la topología, la interpretación cuántica de los campos físicos tales como los campos electromagnéticos y el campo gravitacional, enfocándose sobre los valores de las magnitudes físicas capaces de ser medidos y que no dependen del sistema de coordenadas (cartesianas, polares, esféricas, etc.) tales como la energía de una partícula (estas magnitudes son conocidas en la Mecánica Cuántica como observables), siendo por lo tanto invariantes topológicas, al igual que un cubo es topológicamente igual a una esfera por el hecho de que un cubo de plastilina puede ser moldeado para tomar la forma de una esfera sin necesidad de dividir la masa de plastilina en varias secciones. Se ha descubierto que el polinomio de Jones usado en la teoría matemática de los nudos puede ser generalizado para la elaboración de una TQFT cuyas dimensiones (topológicas) son 2+1 (el 2 corresponde a la dimensión topológica del espacio y el 1 corresponde a la dimensión topológica del tiempo). Los nudos contenidos dentro de este modelo tridimensional (en el sentido topológico) son llamados líneas de Wilson, de las cuales podemos obtener una definición formal en el siguiente enlace:
http://en.wikipedia.org/wiki/Wilson_line
Aunque algunos tópicos en la teoría matemática de los nudos requieren entrar a fondo en teoremas elaborados provenientes de ramas tan sofisticadas como la geometría diferencial y el análisis funcional, no es necesario que los que no sean estudiosos de la materia queden fuera de la acción. En realidad, lo importante para los "legos" es saber que existen otros tipos de aritméticas y álgebras diferentes a lo que está basado en números.
Para aquellos con algo de inclinación hacia las matemáticas interesados en obtener un panorama un poco más amplio sobre algunas de las operaciones básicas utilizadas para el estudio y la clasificación de las propiedades de los nudos, lo puede hacer trasladándose al siguiente enlace mantenido por el departamento de matemáticas de la Universidad de Illinois en Chicago (UIC):
http://www.math.uic.edu/~kauffman/Tots/Knots.htm
que contiene un ensayo elemental de Louis H. Kauffman (uno de los expertos en la materia, precisamente el descubridor del polinomio que lleva su nombre) acerca de la teoría matemática de los nudos. Aquí podrá encontrar el lector más información sobre tópicos tan interesantes como los movimientos Reidemeister, álgebras Lie, las invariantes de Vassiliev, e inclusive algo sobre la teoría topológica de los campos cuánticos (TQFT).
El departamento de matemáticas de la Universidad de California en Irvine (UCI) también mantiene una página en la cual el lector matemáticamente inclinado puede obtener más información acerca de la teoría de nudos:
http://www.ics.uci.edu/~eppstein/junkyard/knot.html
Un curso universitario completo en teoría de nudos ha sido puesto en Internet en el siguiente enlace por el Instituto de Matemáticas de una universidad inglesa, The University of Warwick, cuyos únicos prerequisitos son el álgebra lineal ordinaria que se enseña en los programas de licenciatura así como la capacidad para poder visualizar en tres dimensiones:
http://www.maths.warwick.ac.uk/~bjs/MA3F2-page.html
Si alguno de los lectores de esta exposición desea ponerse "al corriente" en este asunto de la matemática de los nudos, puede dirigirse a dicho sitio para ir asimilando cada una de las lecciones, el cual contiene además exámenes que ya se han administrado ahí en el pasado sobre la teoría de los nudos así como las soluciones a dichos exámenes, con la seguridad de que lo que aquí se ha tratado le servirá para una mejor comprensión de lo que ahí se encontrará. En cuanto a los demás, pueden obtener tanto entretenimiento como un matemático experimentado consiguiéndose un pedazo de cuerda y experimentando con varios tipos de nudos.
Desafortunadamente, no puedo dar más detalles acerca del interesante tema de la teoría matemática de los nudos sin caer en la pedantería, porque este es un tema que se imparte a los matemáticos universitarios a nivel de Maestría e inclusive a nivel de Doctorado, en las escuelas para graduados. Pero ello no detendrá a mis lectores del gusto de tomar un pedazo de cuerda para empezar a construír algunos nudos, y ¿por qué no? tal vez descubrir algo nuevo que se nos ha escapado a todos. A lo mejor uno de mis lectores hasta podría descubrir algo de lo que nadie antes se había dado cuenta, lo cual es posible porque la teoría matemática de los nudos es un asunto inconcluso que todavía sigue siendo objeto de una investigación intensa alrededor del mundo, y continúa siendo (perdonando la expresión), un "nudo gordiano".
No hay comentarios.:
Publicar un comentario